Neural Networks & Symmetry (NetS)
In NetS we design symmetry-aware neural architectures—equivariant convolutions, graph transformers, and physics-informed super-resolution networks—to learn complex scientific data while respecting (or deliberately relaxing) underlying geometric constraints. Our goal is to discover symmetry-breaking factors, encode group invariances, and enhance resolution or expressiveness in high-dimensional physical systems.
Recent highlights include:
• Relaxed group convolution for detecting subtle symmetry breaking in crystals, turbulence, and pendulum dynamics;
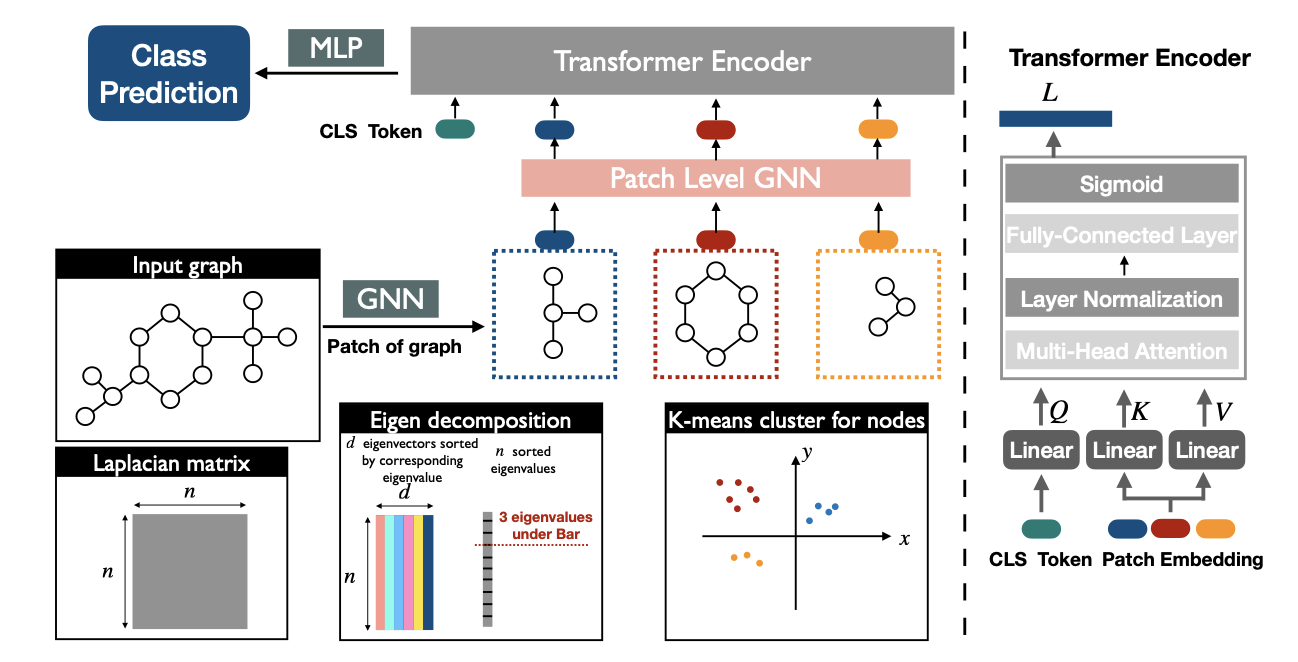
• Patch Graph Transformer (PatchGT) that clusters graphs spectrally and applies transformer attention at the patch level for improved expressiveness and efficiency;
• SSR-VFD — the first deep-learning framework achieving label-free super-resolution of 3-D vector-field data for flow visualization and in-situ compression.
Related Publications
- Wang R., Hofgard E., Gao H., et al. Discovering Symmetry Breaking in Physical Systems with Relaxed Group Convolution, ICML 2024. Link
- Guo L., Ye S., Han J., et al. SSR-VFD: Spatial Super-Resolution for 3-D Vector-Field Data, IEEE TVCG 2020. Link
- Gao H., Han X., Huang J., et al. PatchGT: Transformer over Non-trainable Clusters for Learning Graph Representations, LoG 2022. Link