AI-Accelerated Scientific Computing

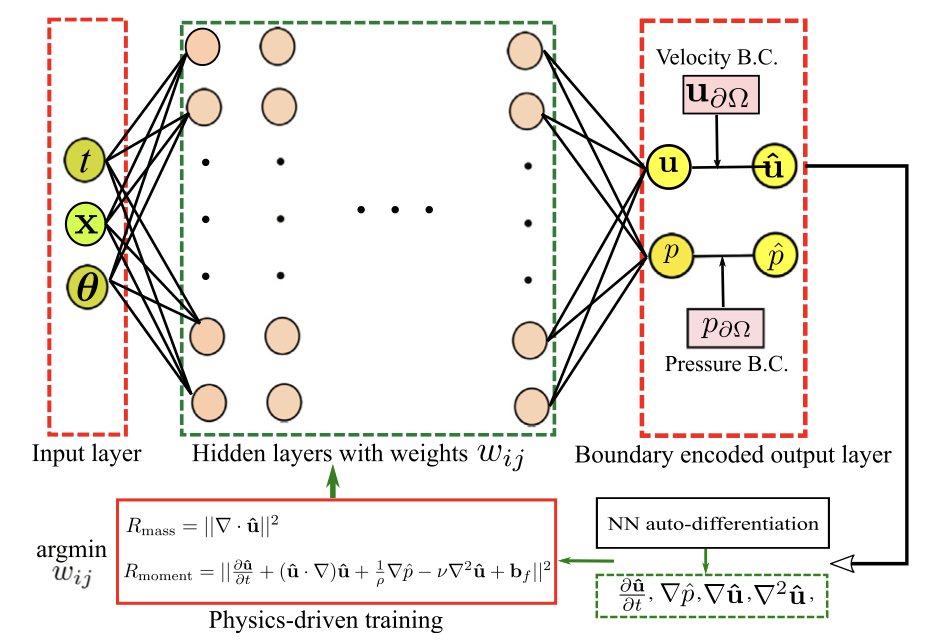
We build physics-informed deep-learning frameworks that unify data-driven learning with numerical discretization, enabling efficient forward and inverse solution of complex PDE systems. Our contributions span:
• Label-free surrogates that learn Navier–Stokes solutions without simulation data;
• Geometry-adaptive CNNs (PhyGeoNet) for irregular domains;
• Graph neural Galerkin networks that combine variational forms with message passing to solve forward & inverse problems;
• Physics-informed super-resolution and denoising of sparse, noisy flow data.

These methods deliver speed-ups and robust generalization across parameters, paving the way for real-time prediction, uncertainty quantification, and design optimization in fluid and multiphysics applications.

Related Publications

• Sun L., Gao H., Pan S., Wang J-X.
  Surrogate Modeling for Fluid Flows Based on Physics-Constrained Deep Learning without Simulation Data. CMAME 361 (2020) 112732. — [Link]
• Gao H., Sun L., Wang J-X.
  PhyGeoNet: Physics-informed Geometry-Adaptive CNNs for Solving Parameterized Steady-State PDEs on Irregular Domains. JCP 428 (2021) 110079. — [Link]
• Gao H., Zahr M.J., Wang J-X.
  Physics-Informed Graph Neural Galerkin Networks: A Unified Framework for Solving PDE-Governed Forward and Inverse Problems. CMAME 390 (2022) 114502. — [Link]
• Sun L., Gao H., Wang J-X.
  Super-Resolution and Denoising of Fluid Flow Using Physics-Informed CNNs without High-Resolution Labels. arXiv 2011.02364 (2020). — [Link]

← Back to Homepage